7.2 Tree Traversal Algorithms
이번 섹션에서는 Tree ADT의 함수를 통해 Tree에 접근하여 traversal computation을 수행하기 위한 알고리즘을 소개한다.
7.2.1 Depth and Height
p를 tree T의 node라고 하자.
- depth : p 자신을 제외한 조상(ancestors)의 수
- 만약 p가 root이면 p의 depth는 0dlek.
- 그렇지 않으면 p의 depth는 p의 parent의 depth에 1을 더한 것과 같다.
- Root의 depth는 0. Depth는 root로부터 얼마나 깊이 있는 지
위 정의에 바탕을 두어, 프로그램 코드 6.3에서 제시된 **recursive algorithm 'depth(T, p)'**는 p의 parent에서 재귀적으로(recursively) 자신(함수)를 호출한 다음, 반환되는 값에 1을 더함으로써 T의 node p의 depth를 계산한다.
// Code Fragment 7.3 : An algorithm to compute the depth of a node p in a tree T
Algorithm depth(T,p):
if p.isRoot() then
return 0
else
return 1+depth(T, p.parent())
depth 알고리즘의 간단한 C++ 구현은 프로그램 코드 7.4와 같다.
// Code Fragment 7.4 : A C++ implementation of the algorithm of Code Frag 7.3
int depth(const Tree& T, const Position& p){
if(p.isRoot())
return 0;
else
return 1+depth(T, p.parent());
}
- 알고리즘 depth(T, p)의 실행시간
알고리즘 depth(T, p)는 p의 각 ancestor에 대해서 상수시간의 recursive step을 수행하기 때문에 **O(d_p)**이다. 여기서 d_p는 트리 T내에서 노드 p의 depth를 의미.
최악의 경우 depth 알고리즘은 O(n) 실행 시간을 갖는다. n은 tree T의 총 node 갯수
하지만 O(d_p)가 더 정확. n보다 작기 때문에
- height : node p의 height 역시 recursively(재귀적으로) 정의된다.
- 만약 p가 외부 노드(external node)이면 p의 height는 0이다.
- 그렇지 않으면 p의 height는 p의 자식의 height 중 가장 높은 값에 1을 더하면 된다.
트리 T의 height는 T의 root의 height이다.
cf) Tree T의 height는 T의 external node의 최대 depth와 같다.
위 명제에 기반하여 tree T의 height를 계산하는 알고리즘 height1(T)를 프로그램 코드 7.5에 제시
//Code Fragment 7.5: Algorithm ****height1(T) for computing the height of a tree T based on computing the macimum depth of the external nodes
Algorithm height1(T):
h=0
for each p∈T.positions() do
if p.isExternal() then
h=max(h, depth(T, p))
return h
위 알고리즘의 C++ 구현은 프로그램 코드 7.6에 제시.
Iterator는 클래스 PositionList의 iterator로 가정한다. 그러한 iterator q가 주어지면 associated position은 *q로 접근 가능.
//Code Fragment 7.6: A C++ implementation of the function height1.
int height1(const Tree& T){
int h=0;
PositionList nodes=T.positions();
for(Iterator q = nodes.begin(); q != nodes.end() ; ++q){
if(q->isExternal)
h=max(h, depth(T, *q));
}
return h;
}
알고리즘 height1은 트리의 height를
알고리즘 height는 트리의 노드 p의 height를..
Code Fragment 7.7: A more efficient algorithm for computing the height of the subtree of tree T rooted at a node p.
Algorithm height2(T , p):
if p.isExternal() then
return 0
else h=0
for each q ∈ p.children() do
h = max(h,height2(T,q))
return 1 + h
7.2.2 Preorder Traversal
Traversal : tree T의 traversal는 T의 모든 노드들을 "방문"하거나 접근하기 위한 체계적인 방법을 뜻한다. 본 절에서는 preorder 순회라 불리는 트리의 기본적인 순회 방식을 소개한다.
⇒ A traversal of a tree T is a systematic way of accessing or "visiting", all the nodes of T
"visit" : node를 방문하는 것(visit)는 traversal이 사용된 application에 따라 다르며, counter를 증가시키는 것부터 각 노드로부터 복잡한 계산을 수행하는 것 까지 포함할 수 있다.
프로그램 코드 7.9는 ‘position p에 의해 참조되는(referenced) node’를 root로 하는 subtree를 preorder traversal 하기 위한 pseudo-code이다.
처음에 preorder(T, T.root())의 형태로 이 루틴을 호출한다.
//code fragment 7.9 : Algorithm preorder for performing the preorder traversal of the subtree of a tree T rooted at a node p
Algorithm preorder(T, p):
perform the "visit" action for the node p
for each child q of p do
recursively traverse the subtree rooted at q by calling preorder(T, q)
preorder traversal 알고리즘은 parent가 항상 children보다 이전 순서에 와야하는 tree node의 linear ordering(순서화)에 유용하다.
preorder traversal은 "모든 노드"를 탐색하기 위한 효과적인 방법
- Big-Oh notation of preorder traversal
— node 하나 방문에 O(1) time 가정
— 각 node p에서 preorder의 nonrecursive part는 O(1+C_p) 시간 소요
— C_p는 p의 children node 수
— 따라서 preorder traversal은 O(n) time 소요 (모든 노드를 한 번씩 방문하므로)
1) preorderPrint(T,p) 함수는 tree T에서 node p의 subtree에 대해서 preorder printing을 실행한다.
- 즉, 그것은 p를 root로 하는 subtree의 preorder traversal을 실행하고, 그 노드가 방문될 때 노드에 저장된 원소를 출력
code fragment 7.10 : Method preorderPrint(T, p) that performs a preorder printing of the elements in the subtree associated with position p of T
void preorderPrint(const tree& T, const Position& p){
cout<<*p;
PositionList ch = p.children();
for(Iterator q = ch.begin(); q!=ch.end(); ++q) {
cout<<" "; //한칸 띠우렴
preorderPrint(T, *q); //자식노드들에 대해 recursive function call
} // iterator을 dereferencing 하면 포지션이다. *q는 iterator q에 상응하는 포지션
}
2) Parenthesis 를 이용한 preorder printing parenPrint(const Tree& T, const Position& p)
void parenPrint(const Tree& T, const Position& P) {
cout<<*p;
if(!p.isExternal) {
cout<<"("
PositionList ch = p.children();
for(Iterator q = ch.begin(); q!=ch.end(); q++ ){
if(q!=ch.begin()) cout<<" ";
parenPrint(T, *q)
}
cout<<")";
}
}
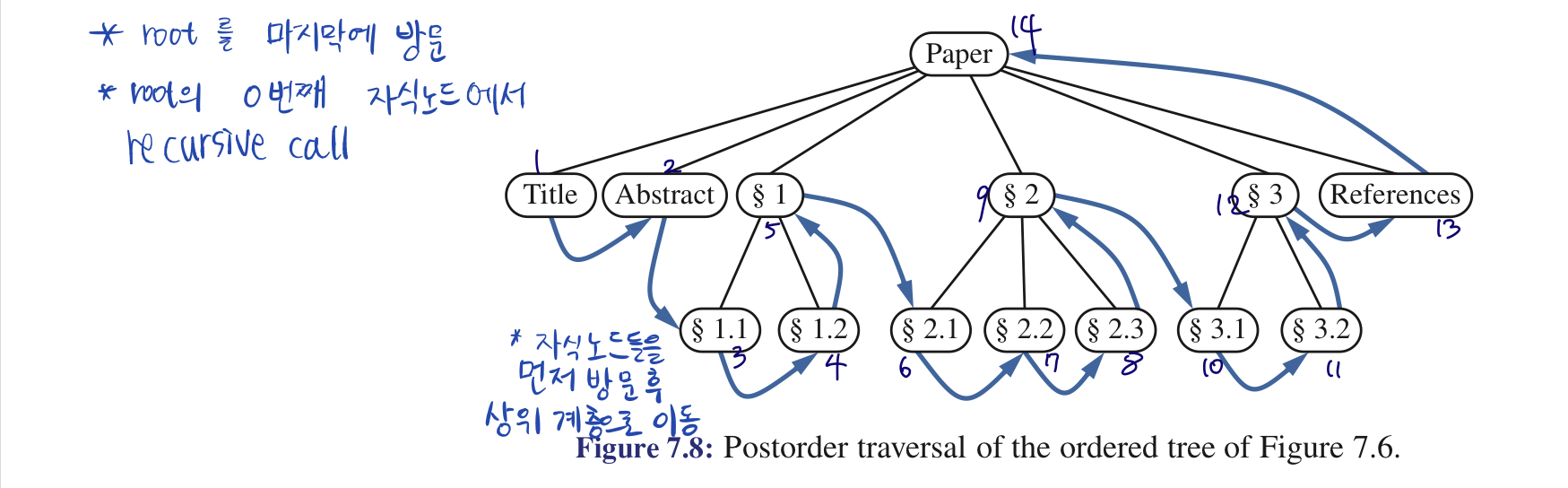
7.2.3 Postorder Traversal
postorder traversal은 root의 childerent들을 root로 하는 subtree 를 먼저 recursively 순회한 후에 root를 방문.
- 알고리즘 pseudo code
Algorithm postorder(T , p):
for each child q of p do
recursively traverse the subtree rooted at q by calling postorder(T, q)
perform the “visit” action for node p
///// 자식노드들에 대해 traverse를 하고 나서 p를 visit
- big-Oh notation of postorder traversal
postorder traversal의 running time은 preorder traversal과 같다. ⇒ O(n)
각 노드들을 방문하는 것은 O(1)
- postorderPrint
code fragment 7.13 : The function postorderPrint(T, p), which prints the elements of the subtree of position p of T
void postorderPrint(const Tree& T, const Position& p) { //tree object T와 tree 내 position p를 reference argument로 받음
PositionList ch = p.children(); // []
for(Iterator q=ch.begin(); q!=ch.end(); q++){ // PositionList의 iterator가 list의 시작부터 마지막 노드까지
postorderPrint(T, *q); // iterator q를 dereferencing 한 것은 그 iterator와 연관된 position이다.
cout<< " ";
}
cout << *p; //자기 자식노드들에 대해 recursive call을 끝내고 자기 자신의 element 프린트!
}
postorder traversal : 트리 안 각 노드 p에서 어떤 계산을 하는 문제에 유리! 그런데 그 계산이 p의 자식에서 이미 계산한 걸 필요로 할 때 유용하다.!!
'전자공학 > 자료구조(정보시스템프로그래밍)' 카테고리의 다른 글
| ch.7 Tree 자료구조 (0) | 2019.06.15 |
|---|---|
| 9.1.1 The Map ADT; 맵의 추상 데이터 타입, 추상 자료형 (0) | 2019.05.12 |
| 9.1 Map : 맵과 맵의 엔트리, 자료구조 맵 맛보기 (0) | 2019.05.10 |
