최근에 코딩을 공부하기 위해서 친구가 추천해준 프로젝트 오일러(Project Euler)의 문제를 순서대로 풀고 있는 중이다.
개인적으로 프로젝트 오일러는 새로운 코딩 언어를 익히기 위해서 굉장히 좋은 도구라고 생각한다. 여기서 문제를 풀면서 다양한 조건문/반복문 사용뿐만 아니라 dynamic programming과 recursive programming 또한 연습할 수 있기 때문이다.
프로젝트 오일러 : https://projecteuler.net/about
About - Project Euler
The page has been left unattended for too long and that link/button is no longer active. Please refresh the page.
projecteuler.net
프로젝트 오일러의 문제를 풀다 보면 굉장히 자주 접하게 되는 문제가 있는데.. 바로바로
1. 소수(prime number) 리스트 구하기
2. 주어진 수가 소수(prime number)인지 판단하기
프로젝트 오일러의 상당수의 문제를 풀 기 위해서는 우선적으로 요 두 가지 문제를 풀어야 했다.
그래서 오늘은 일단, n이하의 소수"prime number"들을 반환하는 알고리즘에 대해서 설명하고 파이썬으로 구현해보기로 한다.

고대 그리스에서도 소수들을 구하기 위해 고군분투 했던 현자가 있는데, 바로바로 에라토스테네스("Eratosthenes")이다. 이 분은 막대기의 그림자로부터 지구의 크기를 측정하신 분으로도 유명하다. (중학교 수학 교과서에 나온다; 후훗 나는 항상 교과과정 중 쓸데없는 것만 기억하는 듯.. ) 아무튼 에라토스테네스의 체(Eratosthenes' Sieve)는 이 분이 소수를 구하기 위해 고안한 방법인데, 꽤 쓸만한 프로그래밍 알고리즘으로 자주 쓰인다.
방법은 매우 간단해서 위키피디아를 읽어봐도 충분하지만, 이 블로그에 공부한 것을 나만의 언어로 바꿔서 써 보는 것 또한 의미 있다고 생각해서 직접 정리해보려고 한다.
문제 정의 : n 이하의 소수들을 구한다.
Specify the problem we can solve easily!!
일반적인 문제 n을 풀기 위해서 n=120인 구체적인 경우를 생각하고 이를 먼저 풀어본다.
왜 에라토스테네스의 '체'라고 부르는 지 곧 알 수 있는데, 왜냐하면 일단 정수들을 나열해 놓고 소수가 아닌 수들을 걸러낼 것이기 때문이다!
0. 방법:
2부터 인덱스를 증가시켜가며, 전체 수 집합에서 해당 인덱스의 배수를 지운다.
해당 인덱스의 배수는 그 인덱스를 약수로 가지므로 소수가 아니기 때문이다!
그리하여 모든 인덱스에 대해 위를 실행하고 최종적으로 남은 수 집합들이 소수 집합이 된다.
1. 자연수 1은 소수가 아니다.
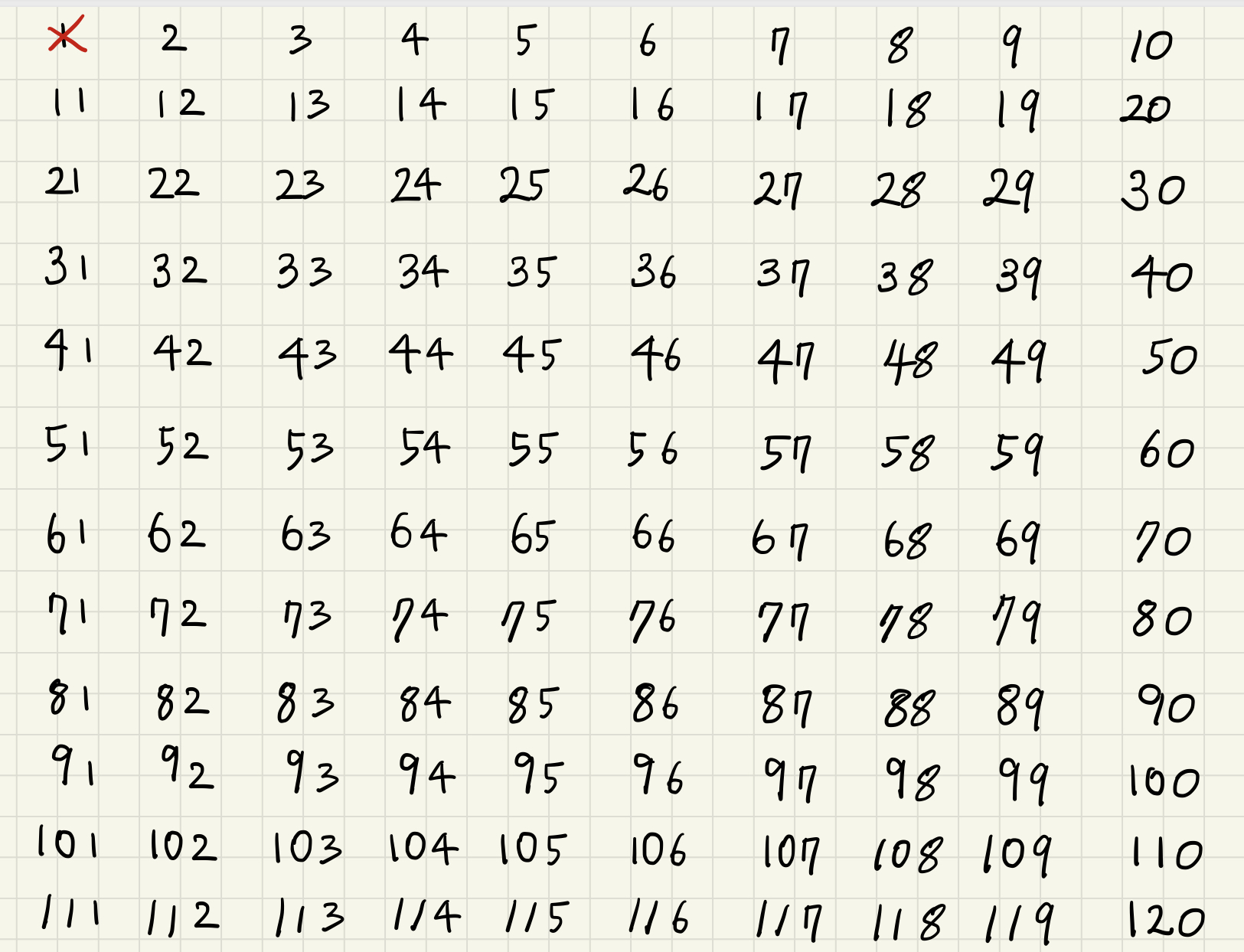
소수의 정의는 "1과 자신만을 약수로 가지는 수"이기 때문이다. 1은 자기 자신도 1이므로 이런 정의에 정합하지 않는다.
2. 첫번째 인덱스 : 2
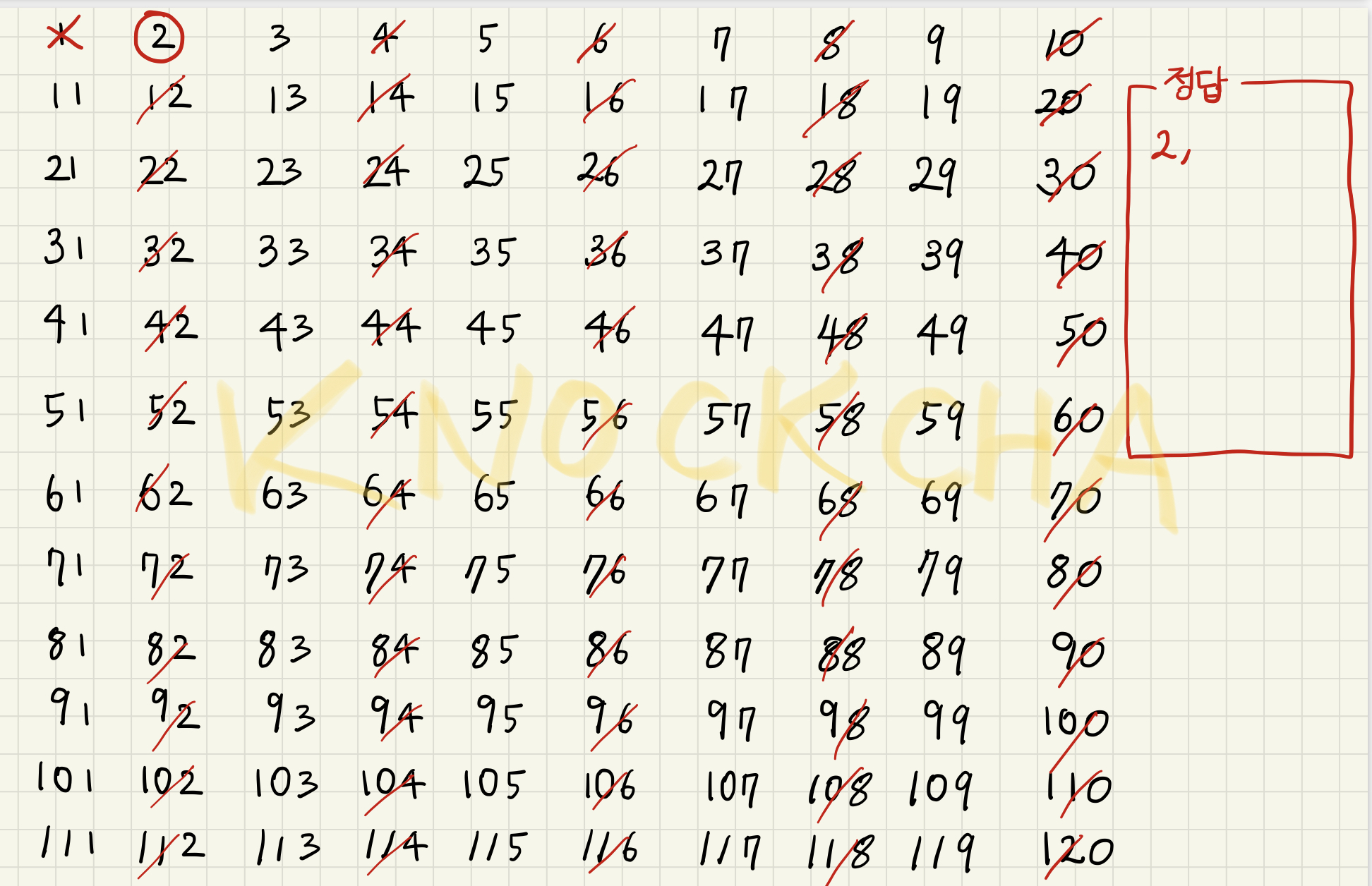
인덱스 2의 배수들을 모두 지운다.
이때 인덱스 2는 소수로 확정된다.
3. 두 번째 인덱스 : 3

첫 번째 인덱스 2의 배수들을 모두 지우고, 인덱스를 증가할 차례이다. 다음 인덱스는 2보다 큰 소수인데, 위와 같이 다음 인덱스는 3이므로 3의 배수들을 남은 집합에서 지워버린다. 그리고 3은 확정된 소수 리스트(Answer!)에 포함시킨다.
4. 세 번째 인덱스 : 5
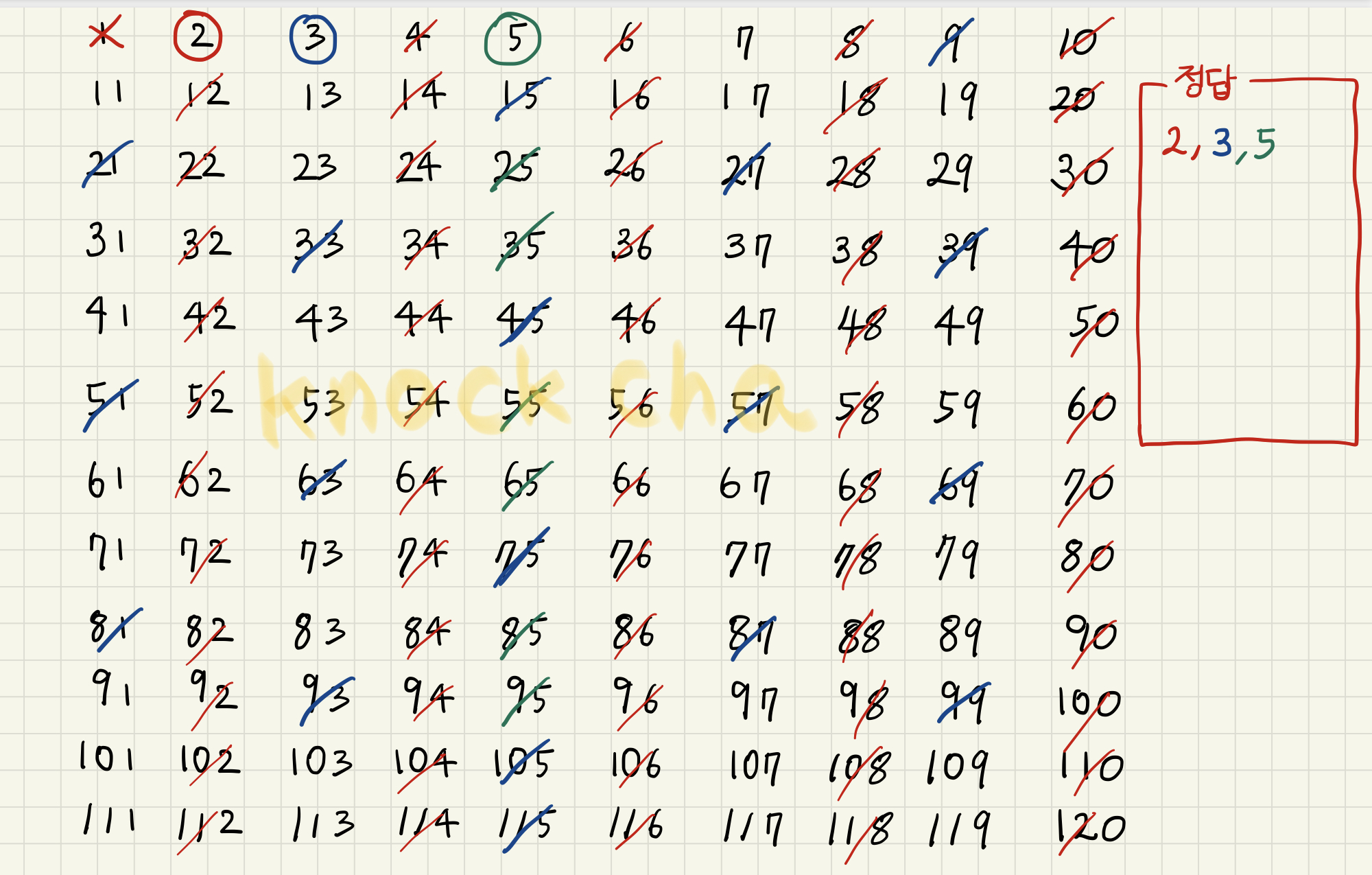
첫 번째와 두 번째 인덱스였던 2와 3의 배수들을 모두 체로 걸러내 버리고 남은 수들 가운데 가장 작은 소수는 5이다. 그러므로 5가 그다음 인덱스가 된다. 마찬가지로 2와 3에 의해 걸러지지 않은 남은 5의 배수들을 걸러버린다.
5. 네 번째 인덱스 : 7
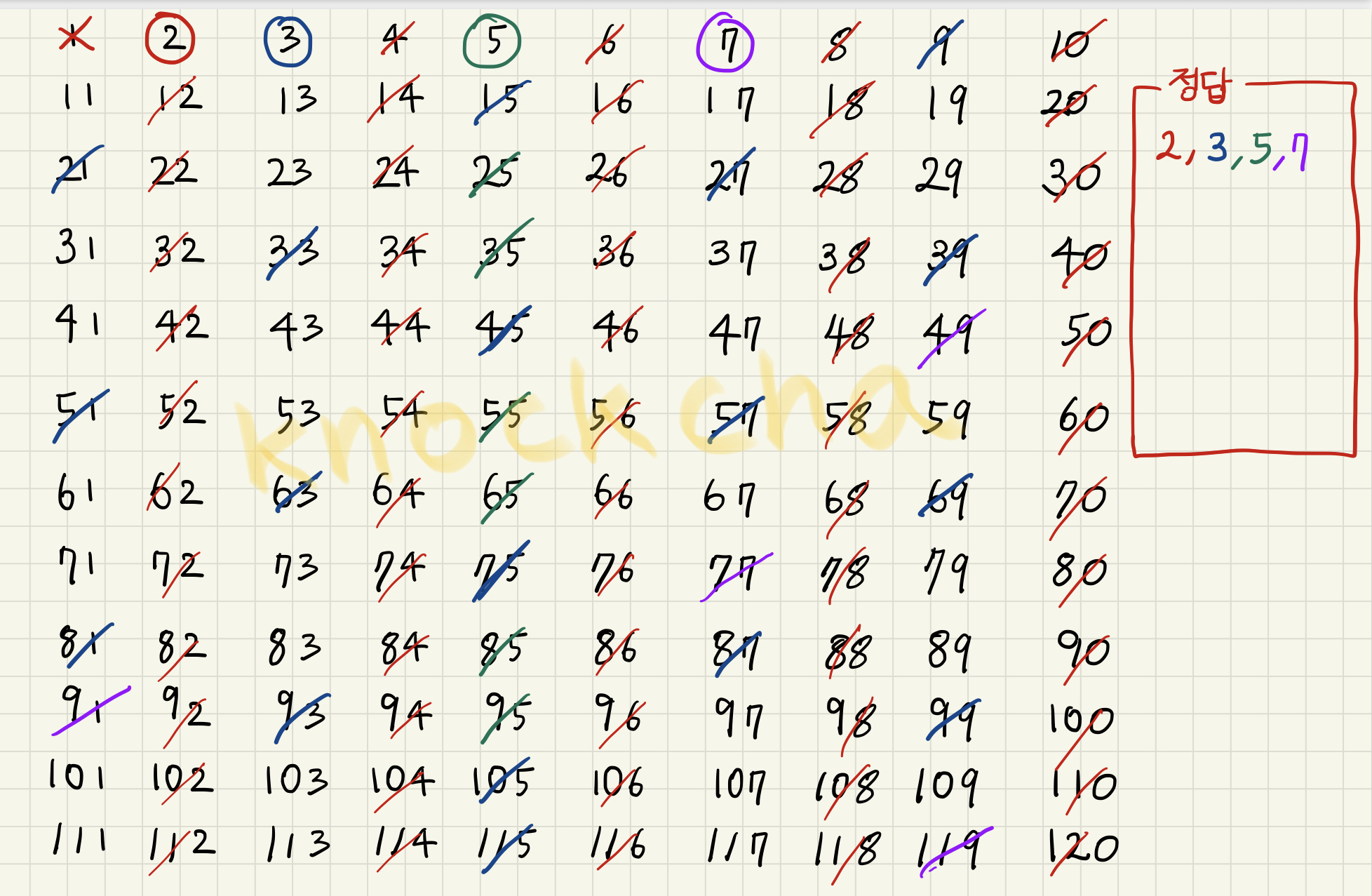
2, 3, 5의 배수들을 전부 걸러버리고 남은 가장 작은 소수는 7이다. 7을 정답 소수 리스트에 포함시키고 7의 배수들도 지워버린다.
6. 다섯 번째 인덱스 : 11
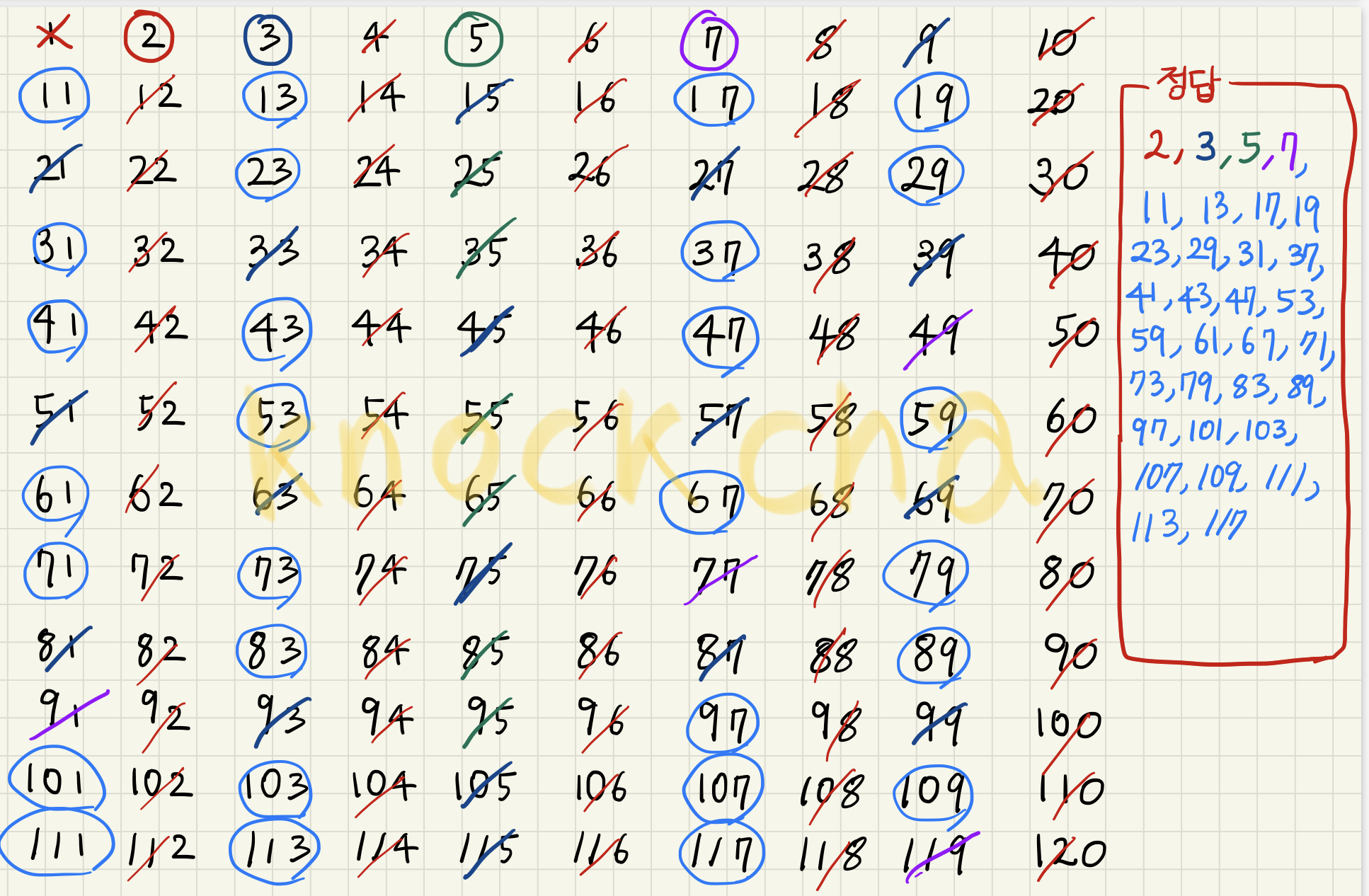
사실 다섯번째 인덱스 11에 관해서는 배수들을 검사하여 걸러낼 필요가 없다. 왜냐하면 11 * x에서 11보다 작은 x들은 이미 이전 인덱스에서 걸러졌기 때문이다. 따라서 인덱스 11에서 걸러지기 시작하는 최소 숫자는 11*11인 121인데, 이는 우리 문제의 범위를 초과한다. 따라서 인덱스 7까지 검사하고, 체에 남은 숫자들을 전부 정답 소수 리스트에 추가한다.
이를 다시 일반적인 문제로 확장한다면...
120이 아닌 n이하의 소수를 구한다고 한다면, 우리는 root(n)의 내림한 정수 인덱스 까지만 검사하면 된다!!!!
파이썬 구현 :
마지막으로 파이썬으로 에라토스테네스의 체를 구현하고 n이하의 소수들을 return(반환)하는 함수를 구현하고 이 글을 마무리 짓는다.
def get_primes(num = 120):
sieve = [True]*num
for i in range(2, int(num**(0.5))):
if sieve[i]:
for x in range(i+i, num, i):
sieve[x] = False
return [k for k in range(2, num) if sieve[k]==True]
print(get_primes())
위 코드에서는 정답 리스트와 체(sieve)를 따로 구현하였다.
sieve = [True]*num
sieve는 n개의 Boolean으로 구성된 1차원 list이며, 해당 인덱스의 수가 소수이면 True를 소수가 아니면 False를 갖는다.
초기화를 위해서 n개 True로 assign된 sieve를 선언해 주었다.
for i in range(2, int(num**(0.5))):인덱스 i는 2부터 시작하여 root(num)의 floor값까지 검사를 한다.
if sieve[i]:
for x in range(i+i, num, i):
sieve[x] = False
만약 내가 고른 인덱스가 소수가 맞다면, 그 인덱스의 배수들 (2*i부터 i씩 더해가며 배수를 얻는다)은 False를 assign 하여 소수가 아니라고 표기한다.
return [k for k in range(2, num) if sieve[k]==True]모든 반복문이 끝난후 True를 갖는 리스트 인덱스들은 소수로 확정된 것이다. 따라서 True를 갖는 리스트의 인덱스만 리스트의 타입으로 리턴한다!
'Programming > Algorithm' 카테고리의 다른 글
| [C언어] assign 연산자의 return 값을 활용한 string copy 함수 만들기 (0) | 2022.04.17 |
|---|---|
| [C언어/파이썬] Insertion Sort Algorithm C와 Python으로 구현해보기 (0) | 2022.04.17 |
| [문제해결 알고리즘] BFS :: 연습문제 :: 미로탈출 로봇 대회(정올) :: C언어 (0) | 2022.01.31 |
| 두 수의 최대 공약수를 구하는 알고리즘 - 유클리드 호제법의 파이썬 구현과 수학적 증명 (0) | 2020.10.01 |

